Matura 2017 – informatyka – rozwiązania
Tegoroczna matura z informatyki nie była łatwa. Zwłaszcza relatywnie trudna wydała mi się teoria, czyli część pierwsza, którą rozwiązuje się bez komputera. Przyjrzałem się tym zadaniom i dałem sobie również ograniczenie czasowe 1h tak jak na maturze.
Oto i rozwiązania…

Zadanie 1 dotyczyło operacji na tablicy liczb całkowitych.
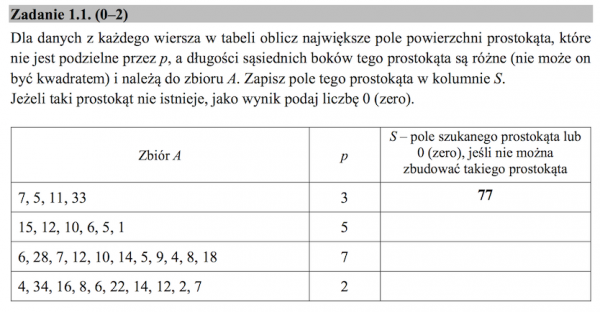
Zadanie 1.1 było raczej proste. Należało znaleźć dwie największe liczby w tablicy, które są niepodzielnie przez zadany parametr p. W przykładzie to oczywiście 11 i 7 (bo 33 jest podzielne przez 3). Dalej to 12 i 6, bo 15 i 10 są podzielne przez 5, więc wynik to 72. W trzecim wierszu to liczby 18 i 12 , bo 28 i 14 są podzielne przez 7, więc wynik to 216. W ostatnim wierszu jest mała pułapka, ponieważ tylko jedna liczba jest niepodzielna przez 2, zatem nie da się stworzyć prostokąta, więc wynik jest 0.

Zadanie 1.2 to napisanie algorytmu, który znajduje te liczby. Zadanie również nie jest banalne. Należy uwzględnić podzielność oraz założyć, że nie istnieje rozwiązanie. Oczywiście nie trzeba jeszcze uwzględniać podzielności samego wyniku, bo p to liczba pierwsza. Gdyby tak nie było komplikowałoby to bardzo algorytm, bo np. składniki mogą nie być podzielne, a ich iloczyn już tak (prosty przykład to dla p=4 mogą być liczby 6 i 10, które same nie są podzielne, ale już ich iloczyn tak). Algorytm zaplanowałbym najpierw ogólnie tak:
- Pętla po tablicy szukająca największą wartość niepodzielną przez p. Wynik zapisać w zmiennej max1
- Jeżeli jej nie ma – zwracamy 0
- Pętla po tablicy szukająca największą wartość, ale mniejszą niż max1 oraz niepodzielną przez p. Wynik zapisać w zmiennej max2
- Jeżeli jej nie ma – zwracamy 0
- Zwracamy max1*max2
Jako schemat blokowy (//EDIT – schemat nie zostałby uznany jako pseudokod), wydaje mi się, że każdy maturzysta z informatyki by sobie już poradził, więc pozwolę sobie go tu nie zamieszczać. Oceniana jest tutaj złożoność obliczeniowa, więc, żeby uzyskać maksymalną punktację, należałoby to zrobić jedną pętlą szukając od razu dwóch największych liczb niepodzielnych przez p. Ale to już nieznaczna modyfikacja algorytmu.
Kolejne zadanie 2.

To funkcja rekurencyjna, która zwraca zmieniony o 1 (gdy x nieparzyste) lub -1 (gdy parzyste) wynik siebie samej podzielonej bez reszty przez 2. Niestety nie jest ona zależna od bezpośrednio poprzednich elementów, co wprowadza dodatkowe zamieszanie. W praktyce to dziwna funkcja, gdzie na szybko nie udało mi się znaleźć reguły zwracającej wyniki. Być może mając więcej czasu udało by się ją znaleźć, więc postanawiam liczyć na piechotę. Dla pewnych wyrazów widać regułę np. licz(2), licz(4), licz(8), licz(16) itd., ale to nie rozwiązuje sprawy. Na spokojnie nie mając ograniczenia czasowego zobaczyłem później, że można się było odnieść do jedynek w wartości binarnej liczby.

W zad. 2.1 należy wyznaczyć 3 wartości tej funkcji. Zatem zostaje żmudne liczenie ręczne i nie liczę po kolei bo szkoda na to czasu. Żeby wyznaczyć te 3 wartości muszę wyznaczyć tylko kilka wartości tej funkcji. Dla sprawdzenia, czy dobrze ją rozumiem liczę przykład dla licz(11) potrzebuję licz(5) oraz licz(2), więc liczę je od końca i zapisuje sobie na przyszłość. Licz(1)=1, licz(2)=0, licz(5)=1, licz(11)=2, więc wychodzi, zatem przystępuję do liczenia dla x=13. Muszę wyznaczyć licz(13), licz(6) oraz licz(3). Zatem od końca licz(3)=2, licz(6)=1, i licz(13) daje wynik 2. Analogicznie postępuję z licz(21), gdzie brakuje mi tylko licz(10) a resztę mam już wcześniej policzone. Szybko zatem wychodzi, że licz(10)=0 a licz(21) daje wynik 1. Dla x=32 muszę policzyć licz(16), licz(8), licz(4), licz(2) co od końca daje ładne wartości 0,-1,-2,-3 zatem licz(32) zwraca wynik -4.
Zadanie nie wydawało się zbyt trudne i nie straciłem na niego dużo czasu.
 Kolejne zadanie na pierwszy rzut oka wydaje się trudne i zapewne wielu się tutaj poddało i strzeliło. Sam po minucie myślenia złapałem się za głowę. Ale na spokojnie zacząłem wyznaczać ile wywołań będzie dla kolejnych x. Zatem dla x=1 jest 1 wywołanie funkcji (k=1). Dla x=2 oraz x=3 wywołań jest 2 (czyli k=2). Dla x=4, x=5, x=6, x=7 wywołań jest 3. Z tego już wprost widać, że dla danego k np. równego 4 najmniejszą wartością x jest 8, czyli 2^3. Odpowiedź prawidłowa zatem to B.
Kolejne zadanie na pierwszy rzut oka wydaje się trudne i zapewne wielu się tutaj poddało i strzeliło. Sam po minucie myślenia złapałem się za głowę. Ale na spokojnie zacząłem wyznaczać ile wywołań będzie dla kolejnych x. Zatem dla x=1 jest 1 wywołanie funkcji (k=1). Dla x=2 oraz x=3 wywołań jest 2 (czyli k=2). Dla x=4, x=5, x=6, x=7 wywołań jest 3. Z tego już wprost widać, że dla danego k np. równego 4 najmniejszą wartością x jest 8, czyli 2^3. Odpowiedź prawidłowa zatem to B.
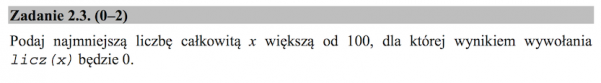
Kolejne zadanie jest naprawdę trudne. Z racji, że nie znalazłem uniwersalnej metody na wyznaczanie licz(x) musiałem liczyć to ręcznie. Zaczynam oczywiście od x=101. Wyznaczam od końca licz(51), licz(25), licz(12). Wychodzi mi licz(25)=1, więc wiadomo już, że wynik nie będzie 0 bo mamy jeszcze 2 zmniejszenia lub zwiększenia wyniku. Przerywam dalsze obliczenia. Analogicznie nie sprawdzam dla x=102, bo tu też wykluczę ze względu na licz(25). Postępuję tam dalej wykluczając wiele niepotrzebnych przeliczeń stosując oczywiste zasady logiki. W niektórych przypadkach wykluczam nawet i 4 wyniki pod rząd, aż dochodzę do x=135. To zadanie zajęło naprawdę dużo czasu i trzeba być naprawdę maksymalnie skupionym, żeby nie popełnić błędu.
Kolejne pytania to pytania testowe z SQL’a. Na żółto zaznaczam prawidłowe odpowiedzi.

Tu raczej nie było podchwytliwych przypadków. Mógł ewentualnie ktoś pomyśleć, że GROUP BY zwraca również posortowane wyniki.

Tutaj teoretycznie też nie ma niespodzianek. No może poza warunkiem 4, gdzie trzeba dostrzec wartość 1 i wykluczający warunek HAVING w zapytaniu.

Tutaj niestety można by się trochę pokłócić z komisją :). Zgodnie ze sztuką zaznaczone powinny być odpowiedzi jak powyżej. Spokojnie jednak można by polemizować czy rozsyłanie wiadomości z serwisu społecznościowego jako „Jan Kowalski” z innym emailem, można by uznać za podszywanie się. Przecież może być wielu Janów Kowalskich. Również w pozycji 4 przy aktualnych zabezpieczeniach wprowadzanych w system DNS i serwery pocztowe tego typu operacja nie bardzo jest możliwa.